We perform inference on a set of unseen excerpts from these same documents. To do so, we
use our trained model on the unobserved documents to determine their respective topic distributions. For each test document, we compare its topic distribution with our training data, and assign its label to the closest match.
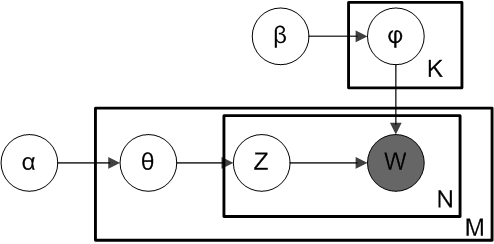
The model can be illustrated in the following chart: phi is topic distribution over all topics, theta is topic distributions for any given document. Both phi and theta are dirichlet distribution with hyper-parameter alpha and beta. W and Z are multinomial distribution likelihood distribution with parameter phi and theta. Therefore, we have two dirichlet-multinomial conjugate pairs: phi-W and theta-Z.
use our trained model on the unobserved documents to determine their respective topic distributions. For each test document, we compare its topic distribution with our training data, and assign its label to the closest match.
The model can be illustrated in the following chart: phi is topic distribution over all topics, theta is topic distributions for any given document. Both phi and theta are dirichlet distribution with hyper-parameter alpha and beta. W and Z are multinomial distribution likelihood distribution with parameter phi and theta. Therefore, we have two dirichlet-multinomial conjugate pairs: phi-W and theta-Z.
In the calculation, we only need conditional distribution of Z, which can be derived from joint probability distribution. Theta will be integrated out and doesn't appear in the conditional probability of Z. This is so called collapsed Gibbs sampler. For detailed derivation, please refer to: http://en.wikipedia.org/wiki/Latent_Dirichlet_allocation
With conditional probability of Z given all the other parameters, we can implement our Gibbs sampler following the algorithm below: